- Proporcionalidad -
Se llama razón entre dos cantidades a y b, a la relación existente entre ambas expresada en forma de cociente indicado.
Se escribe a:b o bien a / b y se lee “a por cada b” o bien “a es a b”.
Cuando la razón entre dos cantidades, a y b, se expresan en forma decimal, se está indicando cuantas veces contiene la cantidad a a la cantidad b (tanto por uno)
Ejemplos:
-
2 kg de patatas por cada Euro
-
200 gramos de pasta por cada comensal
-
6€ por cada 1,5 horas de alquiler de pista
Si dos razones a / b y c / d, son iguales, forman una proporción:
La proporción se leerá “a es a b, como c es a d ”.
Los términos a y d se llaman extremos, y los términos b y c, medios.
Las proporciones se comportan como fracciones equivalentes, por lo que cumplirán:
Vemos en este vídeo los dos casos más habituales que podemos resolver cuando tenemos una proporción.
El primer caso se denomina cuarta proporcional.
El segundo caso se denomina media proporcional.
Puedes practicar proporciones con este juego sin anuncios
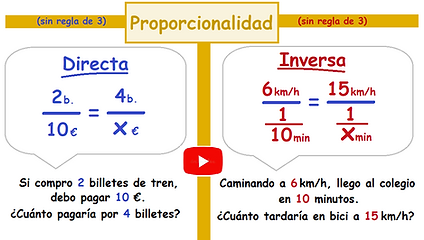
Magnitudes directamente proporcionales
Dos magnitudes, A y B son directamente proporcionales si al multiplicar o dividir por cualquier cantidad una de ellas, la cantidad correspondiente a la otra también queda multiplicada o dividida por dicha cantidad.
Un hecho muy importante que cumplen las magnitudes directamente proporcionales es:
-
El cociente entre cualquier valor de la magnitud B y su correspondiente en A siempre es el mismo y se llama constante de proporcionalidad directa.
En este vídeo, aplicamos las propiedades de dos magnitudes directamente proporcionales para completar una tabla de valores.
Observa que la constante de proporcionalidad será igual a 6.
Métodos de resolución de problemas de proporcionalidad directa
Como véis en el vídeo, son 3 los métodos que podemos emplear:
-
Regla de 3 directa
-
Proporciones
-
Reducción a la unidad
Magnitudes inversamente proporcionales
Dos magnitudes, A y B son inversamente proporcionales si al multiplicar por cualquier cantidad una de ellas, la cantidad correspondiente a la otra también queda dividida por dicha cantidad.
Un hecho muy importante que cumplen las magnitudes inversamente proporcionales es:
-
El producto entre cualquier valor de la magnitud A y su correspondiente en B siempre es el mismo y se llama constante de proporcionalidad inversa.
En este vídeo, aplicamos las propiedades de dos magnitudes inversamente proporcionales para completar una tabla de valores.
Observa que la constante de proporcionalidad será igual a 540.
En los siguientes 2 vídeos analizo los 2 métodos de resolución para problemas con magnitudes inversamente proporcionales (comparando con los métodos usados en proporcionalidad directa)
¿Proporción Directa o Inversa?
Para afrontar con garantías de éxito los problemas de este tema, puede resultaros útil este vídeo para distinguir los casos de proporcionalidad directa o inversa....
Problemas de Proporcionalidad
Un mecanógrafo escribe a 690 pulsaciones cada 3 minutos. ¿Cuántas pulsaciones dará en 8 minutos escribiendo al mismo ritmo?
(Por proporciones y reducción a la unidad)
Un coche ha consumido 32 litros en 400 kilómetros. Suponiendo que el consumo es constante. ¿Cuántos litros consumirá en 650 km?
(Resuelto por proporciones)
Cuatro amigos van al cine y pagan 14,40 € por las entradas. ¿Cuánto les constarán las entradas a un grupo de siete amigos?
(Resuelto por proporciones)
Estudiando 3 horas al día, Alfonso preparó su examen de Natu en 10 días. ¿Cuánto habría tardado en aprenderse el tema estudiando 10 horas diarias?
(Resuelto por regla de 3 inversa)
3 pintores tardan 2 días en pintar una pared. ¿Cuánto tardarán en pintarla 4 pintores al mismo ritmo de trabajo?
(Resuelto por proporciones inversas)
A una velocidad media de 90 km/h un vehículo tarda 40 minutos en realizar un trayecto.
¿Qué velocidad media deberá llevar para realizar el mismo trayecto en 30 minutos?
(Resuelto por proporciones inversas)
Repartos directamente proporcionales
Se basan en una misma estructura según la cual el que más aporta, más recibe (siguen esta proporción)
Un abuelo desea repartir 300 monedas entre sus 3 nietos. No va a darles a todos lo mismo, sino que desea repartirlo de forma directamente proporcional a su edad.
Sabiendo que sus nietos tienen 15, 11 y 4 años respectivamente... ¿Cuánto recibirá cada uno?
Repartos inversamente proporcionales
Se basan en una misma estructura según la cual el que menos aporta, más recibe:
En una prueba deportiva ser reparten 2800 € entre los 2 primeros clasificados en partes inversamente proporcionales a los tiempos invertidos por cada uno, que fuero de 8 y 12 minutos respectivamente.
¿Cuánto corresponde a cada uno?
Proporcionalidad Compuesta
Caso 1: Directa-Directa
Caso 2: Inversa-Directa
Caso 3: Directa-Inversa
Problemas de trabajo simultáneo
Juegos con Proporciones
Practica el cálculo mental de proporciones sencillas con este divertido juego online sin anuncios ni necesidad de registrarse.
Podrás retar a tu profesor... 😎
