
Números Complejos
¿Qué son los números complejos? (vídeo)
Un número complejo es una expresión de la forma a + bi, donde a y b son números reales, e i es un símbolo abstracto, la llamada unidad imaginaria, cuyo significado se explicará más adelante (vídeo). Por ejemplo, 2 + 3i es un número complejo.
En matemáticas, estos números constituyen un cuerpo y se suelen considerar puntos del plano llamado plano complejo. En este plano la parte real nos aporta su coordenada x (abscisa), y la parte imaginaria nos indicaría su coordenada y (ordenada). (vídeo)

Suma y resta de números complejos
Dados dos números complejos a = x + yi y b = u + vi
se suman sumando por separado sus partes reales e imaginarias. Es decir:
a + b = (x + yi) + (u + vi) = (x + u) + (y + v)i
Del mismo modo, la resta se puede realizar como:
a - b = (x + yi) - (u + vi) = (x - u) + (y - v)i
La suma se puede visualizar geométricamente de la siguiente manera: la suma de dos números complejos a y b, interpretados como puntos en el plano complejo, es el punto que se obtiene construyendo un paralelogramo a partir de los tres vértices O, y los puntos de las flechas etiquetadas como a y b (siempre que no estén en una línea).
De manera equivalente, llamando a estos puntos A, B, respectivamente y al cuarto punto del paralelogramo X, los triángulos OAB y XBA son congruentes. (vídeo)

Producto de números complejos
Dados dos números complejos a = x + yi y b = u + vi
Su producto se calcula de la siguiente manera:
a · b = x·u - y·v + (x·v + yu)i
Por ejemplo,
(3 + 2i)·(4 - i) = 3·4 - 2·(-1) + [3·(-1) + 2·4]i = 14 + 5i
Con esta definición llegamos al conocido caso de i^2= -1
Es importante añadir, que la suma y la multiplicación tienen conmutativa, asociativa y distributiva, por lo que los complejos tienen la misma estructura algebraica que los números reales. (vídeo)
Cociente de números complejos
Para dividir números complejos se escribe la división en forma fraccionaria y se multiplican el numerador y el denominador por el conjugado del denominador.
Esto se hace así para que el denominador pase a ser un número real. (vídeo)
Potencia de números complejos
Se utiliza la definición de potencia. Es interesante saber calcular correctamente las potencias de i. No obstante, no se suelen calcular potencias de complejos en forma binómica, sino que se pasan previamente a forma polar.
Ejercicio resuelto:
Forma polar y trigonométrica de un número complejo.
Todo número complejo se puede expresar como un vector OP con origen en el origen de coordenadas, y extremo en su afijo. Queda de esta forma identificado por su módulo r y su argumento alfa. Proyectando ese vector hacia los dos ejes, obtendremos la notación trigonométrica, usando coseno para la proyección horizontal y el seno para la proyección vertical
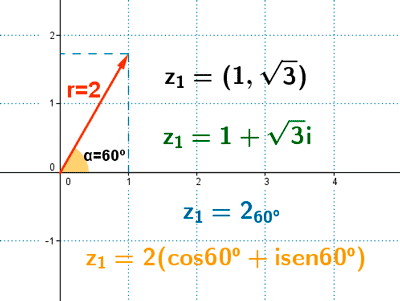
Producto de números complejos en forma polar
La forma polar es extremadamente útil cuando queremos multiplicar o dividir complejos.
El módulo del producto es el producto de los módulos originales y el argumento del producto es la suma de los argumentos originales.
En el caso de la división, cambiaremos a cociente de módulos y resta de argumentos.

Potencias de números complejos en forma polar
Como la potencia es una multiplicación repetida, usaremos la forma de la multiplicación para deducir:

Observa:
-
Si r=1, las potencias sucesivas formarán un círculo al unirlas
-
Si r<1 las potencias formarán una espiral que se cierra.
-
Si r>1 las potencias formarán una espiral que se abre. (animación)
Fórmula de Moivre
Se obtiene al convertir la fórmula de la potencia de un complejo de forma polar a trigonométrica:

Esta fórmula nos permite, entre otras cosas, deducir las fórmulas trigonométricas del ángulo doble (con n=2), triple (n=3) y mitad (n=1/2) de una manera rápida y eficaz.
Raíces de números complejos en forma polar
-Si n es un número natural, se llama raíz n-ésima del número complejo z a todo complejo s tal que s elevado a la n es igual a z.

Observaciones:
-
Tiene n raíces n-ésimas. (Por ejemplo, si es raíz cúbica serán 3 raíces). Alguna de las cuales puede ser un número real (tener argumento 0º)
-
Todas tienen el mísmo módulo, y los argumentos forman una progresión aritmética con diferencia 360/n
-
Si n>2, los afijos de dichas raíces son los vértices de un polígono regular de n lados, inscrito en una circunferencia cuyo radio es el módulo de estas raíces.
Complejos y ecuaciones polinómicas
A diferencia de lo que ocurría con las ecuaciones con coeficientes reales, en el conjunto de los números complejos siempre es posible encontrar las soluciones de cualquier ecuación algebraica. Además, el número de soluciones de una ecuación, coincide con el grado de dicha ecuación. Este resultado fue demostrado por Gauss y recibe el nombre de Teorema fundamental del álgebra, que dice: “Toda ecuación algebraica de grado n, con coeficientes reales o complejos, tiene n raíces en el conjunto de números complejos.”
Ejercicio resuelto:

